그래프의 개념 및 종류
=⇒ 노드와 간선을 이용한 비선형 자료구조
목적에 따라 간선의 가중치나 방향이 있을 수 있음

그래프의 구현
인접 행렬
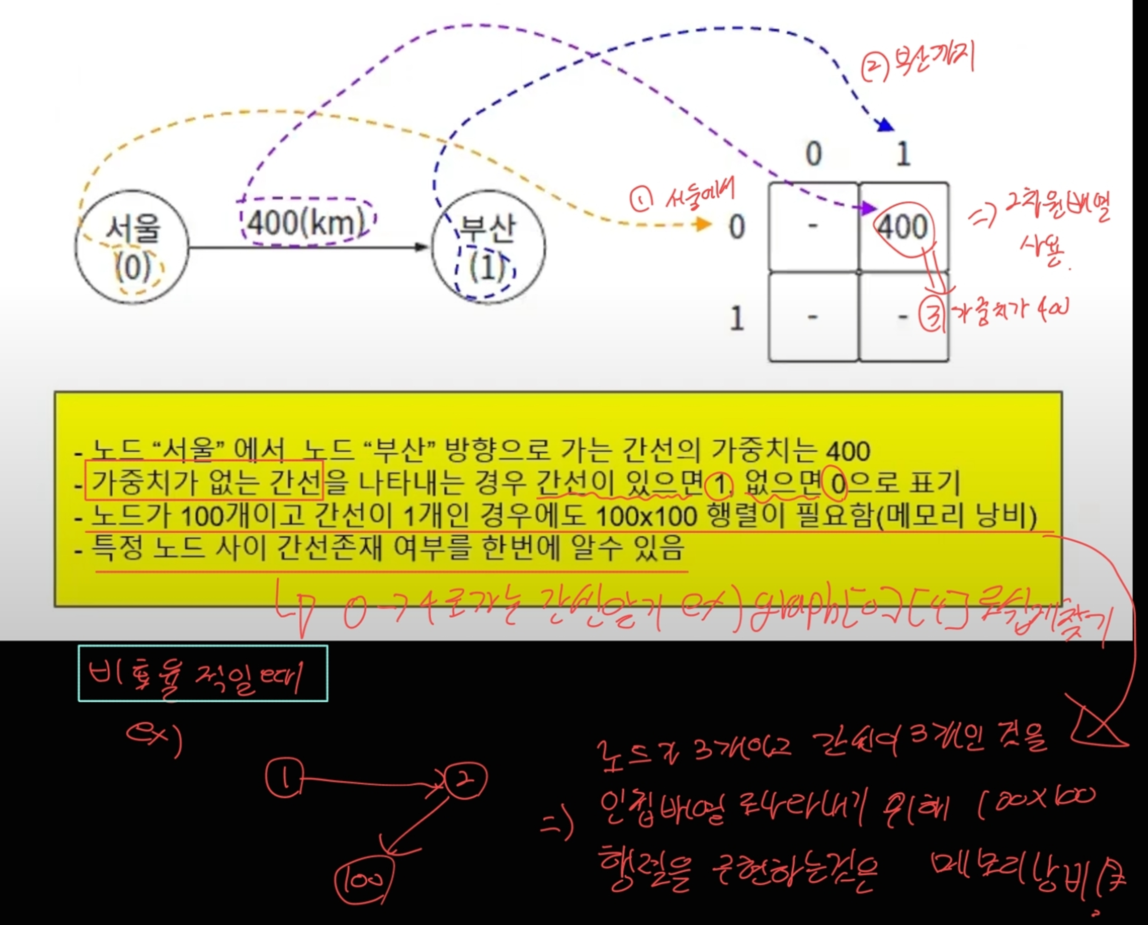
#include <iostream>
using namespace std;
// 인접 행렬의 노드 개수 (고정)
const int numNodes = 2;
// 인접 행렬 배열
int adjMatrix[numNodes][numNodes];
/*최악의 경우 1 -> 2 -> 100 일때 100*100의 배열을 만들어야함*/
//그래프 초기화
void initializeMatrix() {
for (int i = 0; i < numNodes; i++) {
for (int j = 0; j < numNodes; j++) {
adjMatrix[i][j] = 0;
}
}
}
// 간선을 추가하는 함수
// u(시작노드)에서 v(도착노드)로 가는 간선의 가중치를 설정
void addEdge(int u, int v, int weight) {
adjMatrix[u][v] = weight;
}
// 인접 행렬을 출력하는 함수
// 값이 0인 경우 '-'로 출력
void printMatrix() {
for (int i = 0; i < numNodes; i++) {
for (int j = 0; j < numNodes; j++) {
if (adjMatrix[i][j] == 0)
cout << "- ";
else
cout << adjMatrix[i][j] << " ";//실제 가중치 출력
}
cout << endl;
}
}
int main() {
// 인접 행렬 초기화
initializeMatrix();
// 엣지 추가: 서울(0)에서 부산(1)으로 가는 엣지, 가중치 400
addEdge(0, 1, 400);
// 인접 행렬 출력
printMatrix();
/*
최종적인 인접 행렬의 모습:
- 400
- -
*/
return 0;
}
/*
인접 행렬의 시간 복잡도:
- 인접 행렬을 사용하여 그래프를 표현할 경우, 공간 복잡도는 O(V^2)입니다.
-->여기서 V는 노드의 개수입니다.
- 간선이 존재하는지 확인하는 작업은 O(1)의 시간 복잡도를 가집니다.
- 모든 간선을 탐색하는 작업은 O(V^2)의 시간 복잡도를 가집니다.
최종적인 인접 행렬의 모습:
- 400
- -
*/인접 리스트
⇒특정 시작 노드를 기준으로 연결된 노드들을 리스트로 연결하는 방식.
⇒실제 그래프의 노드 갯수 만큼만 추가하므로 인접행렬과는 다르게 메모리 낭비가 없다
⇒특정 노드에 모든 노드가 연결된 경우, 탐색시 O(N) (거의 드물다,)
⇒동적 그래프: 간선의 추가와 삭제가 상대적으로 용이합니다.
- 인접 리스트 표현방식
- 노드 개수 만큼 배열을 준비한다.
- 각 배열의 인덱스는 시작 노드를 나타냄, 해당 인덱스에 연결된 노드 추가


#include <iostream>
#include <vector>
using namespace std;
int main() {
// 정점의 수
int V = 4;
// 인접 리스트 생성
vector<pair<int, int>> adjList[V + 1];
//도착노드, 가중치 (pair사용)
// 그래프에 간선 추가
adjList[1].push_back({2, 3});
adjList[1].push_back({3, 5});
adjList[2].push_back({1, 6});
adjList[2].push_back({3, 5});
adjList[3].push_back({2, 1});
adjList[3].push_back({4, 13});
adjList[4].push_back({4, 9});
adjList[4].push_back({1, 42});
//시작 // 도착노드, 가중치
// 인접 리스트 출력
for (int i = 1; i <= V; ++i) {
cout << "Vertex " << i << ":";
for (auto edge : adjList[i]) {
cout << " (" << edge.first << ", " << edge.second << ")";
//도착노드 //가중치
}
cout << endl;
}
return 0;
}
/*
인접리스트의 개념:
- 인접리스트는 그래프를 표현하는 방법 중 하나로, 각 정점에 연결된 다른 정점들을 리스트 형태로 저장합니다.
이 리스트는 일반적으로 벡터, 배열 또는 링크드 리스트로 구현됩니다.
인접리스트의 시간 복잡도:
- 그래프의 모든 간선을 순회하는데 걸리는 시간은 O(E)입니다.
여기서 E는 간선의 수를 의미합니다.
- 정점의 수를 V라 할 때, 모든 정점을 순회하는데 O(V)의 시간이 걸립니다.
- 특정 정점에 연결된 모든 정점을 순회하는 시간은 해당 정점에 연결된 간선의 수에 비례하며,
평균적으로 한 정점에 연결된 간선의 수는 E/V이므로 O(E/V)입니다.
- 따라서, 그래프 전체를 순회하는 시간 복잡도는 O(V + E)입니다.
이는 각 정점과 각 간선을 한 번씩 방문하는 것을 의미합니다.
완성된 인접리스트의 모습:
- 위 코드에서 출력되는 인접리스트는 다음과 같은 형식을 가집니다.
Vertex 1: (2, 3) (3, 5)
Vertex 2: (1, 6) (3, 5)
Vertex 3: (2, 1) (4, 13)
Vertex 4: (4, 9) (1, 42)
*/
인접 행렬 VS 인접 리스트

⇒노드의 갯수가 많을 때는 인접 리스트 사용 (메모리 초과 가능성 때문에)
⇒특정 정점의 간선을 찾는 경우가 많으면 인접 행렬 사용 고려
⇒뭘 써야 할지 모른다면 인접 리스트를 사용하는 것이 유리해 보임!
그래프의 탐색
⇒그래프를 정해진 순서로 순회하는 방법
- 깊이 우선 탐색 - DFS
- 더 이상 탐색할 노드가 없을 때까지 일단 간다.
- 더 이상 탐색할 노드가 없으면 최근에 방문했던 노드로 돌아간 뒤(백트래킹), 가지 않은 노드를 방문한다
- 너비 우선 탐색 -BFS
- 현재 위치에서 가장 가까운 노드부터 방문하고 다음 노드로 넘어감
- 모든 노드를 방문할 때까지 위 과정 반복
깊이 우선 탐색 - DFS
=> DFS는 그래프 탐색 알고리즘 중 하나로, 시작 정점에서 출발하여 한 방향으로 가능한 깊이까지 탐색한 후, 더 이상 갈 곳이 없으면 이전 정점으로 되돌아와 다른 방향으로 탐색을 계속하는 방식이다.

구현해야 할 동작
- 계속해서 깊이 탐색할 수 있어야함.
- 백트래킹 구현(가장 최근에 방문했던 노드로 퇴각)
- 백트래킹 효율적인 방법
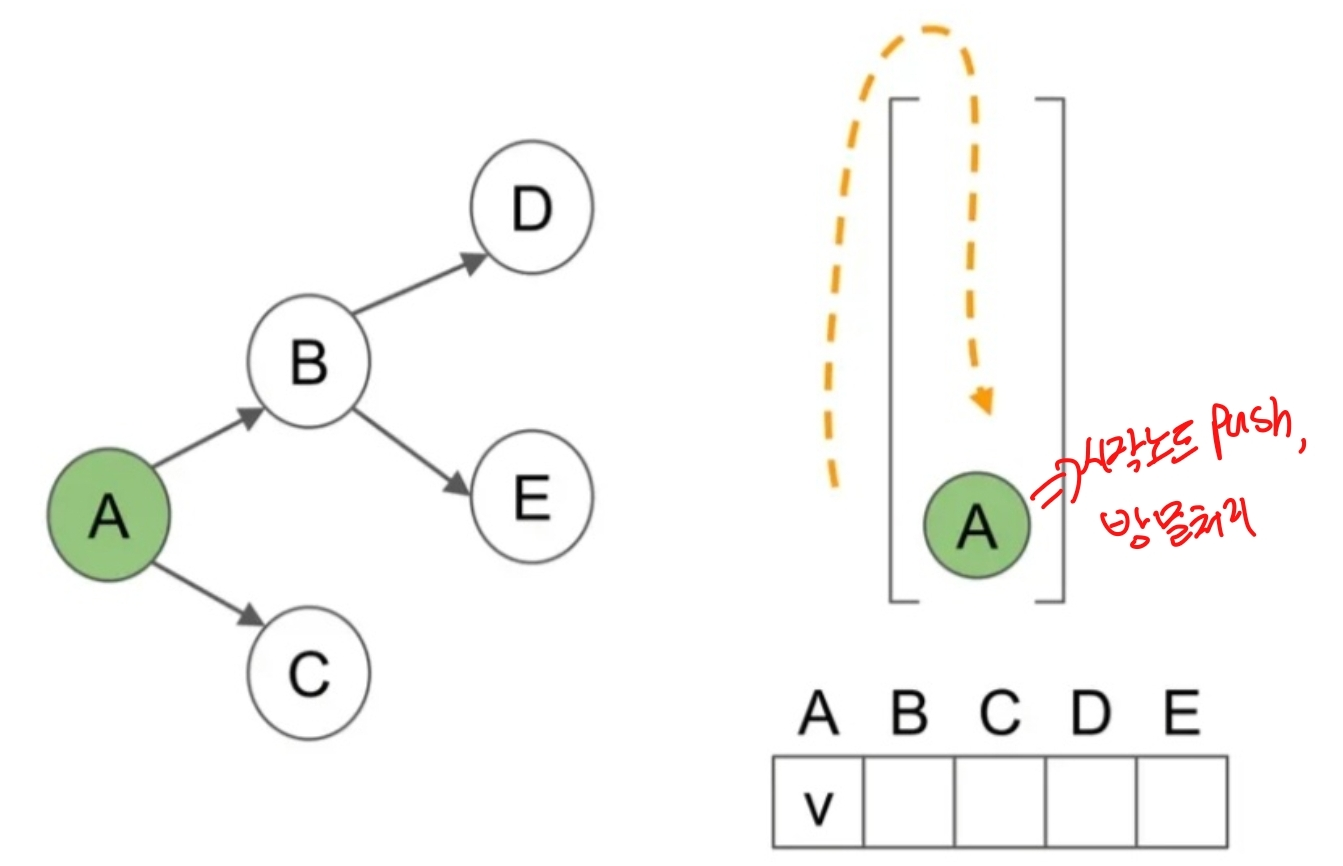
- 스택 활용
- 방문할 노드는 push, 방문한 노드는 pop하면 스택의 TOP은 가장 최근에 방문한 노드!
- 함수의 call stack도 stack과 같이 동작하므로 재귀함수로 구현하는 경우가 많다.
- visited 배열을 활용해서 방문 여부를 확인 후 방문함.
- 백트래킹 효율적인 방법
- 이미 방문한 노드는 중복해서 방문 X
#include <iostream>
#include <vector>
using namespace std;
// 전역 인접 리스트
vector<vector<int>> adj;
//방문한 노드 리스트
vector<bool> visited;
// 그래프에 간선을 추가하는 함수
// 인자: v (정점), w (연결된 정점)
void add_edge(int v, int w) {
adj[v].push_back(w); // 정점 v의 인접 리스트에 정점 w를 추가
}
// 깊이 우선 탐색(DFS)을 수행하는 함수
// 인자: v (현재 정점)
void dfs(int v) {
// 현재 정점을 방문했다고 표시하고 출력
visited[v] = true;
cout << v << " ";
// 현재 정점에 인접한 모든 정점을 순회
for (int i = 0; i < adj[v].size(); ++i) {
if (!visited[adj[v][i]]) {//방문하지 않았다면?
dfs(adj[v][i]);//dfs실행
}
}
}
// 메인 함수: 그래프 생성 및 DFS 수행
int main() {
// 정점의 개수
int V = 5;
adj.resize(V);
// 그래프에 간선 추가 (주어진 다이어그램에 따라)
add_edge(0, 1); // A -> B
add_edge(0, 2); // A -> C
add_edge(1, 3); // B -> D
add_edge(1, 4); // B -> E
cout << "깊이 우선 탐색 (정점 0에서 시작):\n";
visited.assign(V, false);//방문 리스트 초기화
dfs(0);
/*
재귀 호출 과정 설명 (예: 정점 0에서 시작):
dfs(0) 호출 -> 0 출력
dfs(1) 호출 -> 1 출력
dfs(3) 호출 -> 3 출력
dfs(4) 호출 -> 4 출력
dfs(2) 호출 -> 2 출력
- dfs_traversal 종료
*/
return 0;
}
/*
- 시간 복잡도는 O(V + E)이며, 여기서 V는 정점의 수, E는 간선의 수를 의미한다.
*/
- DFS를 사용해야 하는 경우:
- 그래프의 모든 정점을 방문해야 하는 경우
- 경로 찾기 (예: 미로 탐색)
- 사이클 검출
- 위상 정렬
- 강한 연결 요소 찾기
- BFS를 사용할 수 없고 DFS를 사용해야 하는 경우:
- 재귀적 성질을 이용해야 할 때 (예: 백트래킹 문제)
- 공간 복잡도가 중요한 경우 (BFS는 큐를 사용하여 더 많은 메모리를 필요로 함)
DFS 동작 방식




너비 우선 탐색 - BFS
⇒ 시작 정점에서 출발하여 인접한 모든 정점을 먼저 탐색한 후, 다음 깊이의 정점들을 탐색

구현해야 할 동작
- 루트노드부터 시작해서 가장 가까운 노드들부터 방문할 수 있어야함.
- ⇒ 루트노드방문 → 1개 간선으로 갈 수 있는 노드 방문 → 2개 간선으로 갈 수 있는 노드방문 ….모든 노드를 방문할 때 까지 반복
- 가장 가까운 노트부터 방문하는 효율적인 방법
- 큐 활용.
- 시작 노드 푸시
- pop 후에 방문처리 이후, 현재 노드에서 연결된 노드 중 방문하지 않은 노드 모두 push
- ⇒모든 노드를 방문할 때까지 2번반복
- 큐 활용.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// 전역 인접 리스트 및 방문 리스트
vector<vector<int>> adj;
vector<bool> visited;
// 그래프에 간선을 추가하는 함수
// 인자: u (정점), v (연결된 정점)
void add_edge(int u, int v) {
adj[u].push_back(v); // 정점 u의 인접 리스트에 정점 v를 추가
}
// 너비 우선 탐색(BFS)을 수행하는 함수
// 인자: start (시작 정점)
void bfs(int start) {
queue<int> q;
visited[start] = true;//시작노드 방문여부 true
q.push(start);
while (!q.empty()) {
int v = q.front();
q.pop();
cout << v << " ";
for (int i = 0; i < adj[v].size(); ++i) {
if (!visited[adj[v][i]]) {
visited[adj[v][i]] = true;
q.push(adj[v][i]);
}
}
}
}
// 메인 함수: 그래프 생성 및 BFS 수행
int main() {
// 정점의 개수
int V = 5;
adj.resize(V);
// 그래프에 간선 추가 (주어진 다이어그램에 따라)
add_edge(0, 1); // A -> B
add_edge(0, 2); // A -> C
add_edge(1, 3); // B -> D
add_edge(1, 4); // B -> E
cout << "너비 우선 탐색 (정점 0에서 시작):\n";
bfs(0);
/*
BFS 호출 과정 설명 (예: 정점 0에서 시작):
1. bfs(0) 호출 -> 0 출력, 인접 정점 1과 2를 큐에 추가
2. 큐에서 1을 꺼내어 출력 -> 인접 정점 3과 4를 큐에 추가
3. 큐에서 2를 꺼내어 출력 -> 인접 정점 없음
4. 큐에서 3을 꺼내어 출력 -> 인접 정점 없음
5. 큐에서 4를 꺼내어 출력 -> 인접 정점 없음
6. 큐가 비어 있으므로 탐색 종료
*/
return 0;
}
/*
- BFS는 큐를 사용하여 구현되며, 시간 복잡도는 O(V + E)이다.
여기서 V는 정점의 수, E는 간선의 수를 의미한다.
*/
BFS를 사용해야 하는 경우
- 최단 경로를 찾아야 하는 경우 (예: 최단 경로 문제)
- 레벨 순서 탐색을 해야 하는 경우 (예: 각 레벨별로 노드를 처리해야 하는 문제)
- 사이클 검출 (무방향 그래프에서)
DFS 대신 BFS를 사용해야 하는 경우
- 경로의 길이가 중요한 경우 (BFS는 최단 경로를 보장함)
- 큐를 사용하여 더 적은 메모리로 처리가 가능한 경우 (특히 넓은 그래프에서)
- 모든 정점을 같은 레벨에서 순서대로 처리해야 하는 경우
BFS 동작 방식



DFS VS BFS
- 백트래킹 ⇒ 깊이우선 탐색에만 존재
- 스도쿠문제 OR 1~5를 사용해서 합이 10이되는 경우..
- 너비우선 탐색으로 찾은 해만 최적해를 보장
- 시작점에서 끝지점 까지 가는데 최소 스텝수
- ⇒ 너비우선 탐색을 사용해 해를 찾으면 가장 가까운 노드부터 탐색을 하기 때문에 최적해가 보장이 된다. 만약에 깊이 우선으로 찾게 되면 일단 먼저 가장 깊은 노드까지 가서 찾기 때문에 최소 스텝수를 보장하지 않는다
- 너비우선 탐색은 모든 다음노드를 큐에 push하므로 깊이우선 탐색보다 메모리 사용량이 높음
- 애매하면 깊이우선 탐색부터 먼저 시도...
최단경로 알고리즘
⇒두 노드를 잇는 가중치의 합을 최소로 하는 경로를 찾음

→가중치가 없을때 : 1 → 5 가 최단경로(간선이 1개)
→가중치가 있을때 : 1→4→5 (가중치가 가장 작은 경로)
다익스트라 알고리즘
- 다익스트라 알고리즘의 개념: 다익스트라 알고리즘은 가중치가 있는 그래프에서 특정 시작 노드로부터 다른 모든 노드까지의 최단 경로를 찾는 알고리즘입니다. 이 알고리즘은 그래프의 모든 간선의 가중치가 양수일 때 유효합니다.
- 다익스트라 알고리즘의 과정:
- 시작 노드의 거리를 0으로 설정하고, 나머지 노드의 거리는 무한대로 설정합니다.
- 모든 노드를 미방문 집합에 추가합니다.
- 현재 노드에서 인접한 모든 노드의 거리를 계산하여 더 짧은 경로가 발견되면 거리를 업데이트합니다.
- 현재 노드를 방문한 것으로 표시하고, 미방문 노드 중 최단 거리를 가진 노드를 선택하여 3) 과정을 반복합니다.
- 모든 노드를 방문할 때까지 3)과 4) 과정을 반복합니다.
- 다익스트라 알고리즘 시간 복잡도
- 인접 리스트를 사용한 구현: O((V+E)log V), 여기서 V는 노드의 개수, E는 간선의 개수입니다. (우선순위 큐를 사용하여 최소 거리를 찾고 업데이트하는데 log V 시간이 걸립니다)
- 다익스트라 알고리즘의 한계
- ⇒음수 가중치를 가진 간선이 있는 그래프에서는 동작 x —>벨만 포드 알고리즘을 사용해야함
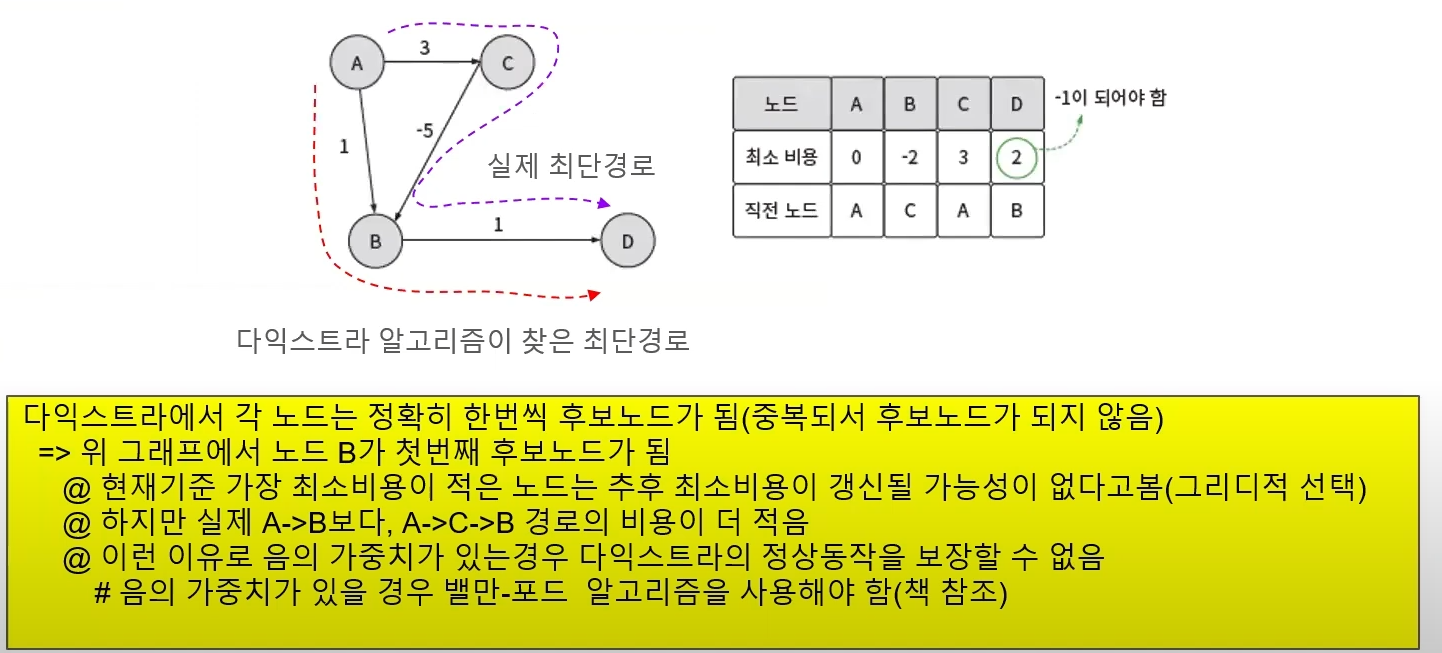
다익스트라 알고리즘으로 실제 최단 경로 구하기







다익스트라 알고리즘의 구현
후보노드는 현재까지 후보가 되지 않았던 노드 중, 최소비용이 가장 적은 노드
⇒ visited배열을 사용해 방문 여부를 체크함
⇒ 최고 비용이 가장 적은 노드는 우선 순위 큐를 활용해서 확인
- 최소비용이 갱신된 노드는 우선 순위 큐에 푸시
- 우선순위큐에서 pop을 할때 visited를 활용해 이미 방문여부를 확인
- 방문 했다면 아무동작 x
- 방문 안했다면 최소비용 갱신함.
#include <iostream>
#include <vector>
#include <queue>
#include <utility>
#include <limits>
using namespace std;
// 무한대를 나타내기 위해 사용되는 상수
const int INF = numeric_limits<int>::max();
// 전역 변수 선언
vector<vector<pair<int, int>>> graph; // 그래프를 인접 리스트 형태로 저장
vector<int> dist; // 각 노드까지의 최단 거리를 저장
vector<int> prev; // 각 노드의 직전 노드를 저장
vector<bool> visited;
// 다익스트라 알고리즘 함수
void dijkstra(int start) {
int n = graph.size(); // 그래프의 노드 개수
dist.assign(n, INF); // 최단 거리 배열을 무한대로 초기화
prev.assign(n, -1); // 직전 노드 배열을 -1로 초기화
dist[start] = 0; // 시작 노드의 거리는 0으로 설정
// 최소 힙 (우선순위 큐)을 사용하여 최단 거리를 찾음
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, start}); // 시작 노드를 큐에 추가
// 초기 상태
/*
Initial state:
Node: A B C D E
Dist: 0 INF INF INF INF
Prev: -1 -1 -1 -1 -1
*/
// 큐가 빌 때까지 반복
while (!pq.empty()) {
int d = pq.top().first; // 현재 노드까지의 거리
int u = pq.top().second; // 현재 노드
pq.pop(); // 큐에서 제거
// 현재 노드까지의 거리가 이미 더 짧은 경로가 있으면 무시
if (visited[u]) continue;
visitied[u] = true;
// 현재 노드의 모든 인접 노드를 탐색
for (const auto& edge : graph[u]) {
int v = edge.first; // 인접 노드
int weight = edge.second; // 가중치
// 더 짧은 경로를 발견한 경우
if (dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight; // 최단 거리 업데이트
prev[v] = u; // 직전 노드 업데이트
pq.push({dist[v], v}); // 큐에 추가
}
}
}
}
// 경로를 출력하는 함수 (재귀 호출 사용)
void printPath(int node) {
if (node == -1) return; // base case: 시작 노드에 도달
printPath(prev[node]); // 직전 노드로 재귀 호출
cout << node << " "; // 현재 노드 출력
}
// 다익스트라 알고리즘 수행 과정 주석
/*
Initial state:
Node: A B C D E
Dist: 0 INF INF INF INF
Prev: -1 -1 -1 -1 -1
1. A 노드 선택 (현재 최단 거리: 0)
- 인접 노드 B, C, E 업데이트:
After visiting A:
Node: A B C D E
Dist: 0 4 4 INF 1
Prev: -1 0 0 -1 0
2. E 노드 선택 (현재 최단 거리: 1)
- 인접 노드 C 업데이트:
After visiting E:
Node: A B C D E
Dist: 0 4 3 INF 1
Prev: -1 0 4 -1 0
3. C 노드 선택 (현재 최단 거리: 3)
- 인접 노드 B, D 업데이트:
After visiting C:
Node: A B C D E
Dist: 0 4 3 11 1
Prev: -1 0 4 2 0
4. B 노드 선택 (현재 최단 거리: 4)
- 인접 노드 업데이트 없음
After visiting B:
Node: A B C D E
Dist: 0 4 3 11 1
Prev: -1 0 4 2 0
5. D 노드 선택 (현재 최단 거리: 11)
- 인접 노드 B 업데이트:
After visiting D:
Node: A B C D E
Dist: 0 4 3 11 1
Prev: -1 0 4 2 0
최종 상태:
Node: A B C D E
Dist: 0 4 3 11 1
Prev: -1 0 4 2 0
*/
/*
코드 실행 결과:
Node Distance Path
0 0 0
1 4 0 1
2 3 0 4 2
3 11 0 4 2 3
4 1 0 4
*/
int main() {
// 그래프를 인접 리스트 형태로 정의
// 각 pair는 (인접 노드, 가중치)를 의미
graph = {
{{1, 4}, {2, 4}, {4, 1}}, // A (0)
{}, // B (1)
{{1, 6}, {3, 8}}, // C (2)
{{1, 2}}, // D (3)
{{2, 2}} // E (4)
};
int start = 0; // 시작 노드 (A)
dijkstra(start); // 다익스트라 알고리즘 실행
// 결과 출력
cout << "Node\tDistance\tPath" << endl;
for (int i = 0; i < dist.size(); ++i) {
cout << i << "\t" << dist[i] << "\t\t";
printPath(i);
cout << endl;
}
return 0;
}
출처
[지금 무료] 코딩 테스트 합격자 되기 - C++ 강의 | dremdeveloper - 인프런
dremdeveloper | 코딩 테스트 합격을 위한 C++ 강의, 책 없이도 가능! 저자와 직접 소통 가능한 커뮤니티 제공!, [사진]여기에 문의 하세요https://open.kakao.com/o/gX0WnTCf📘 코딩 테스트 합격자 되기 - C++편
www.inflearn.com
'Algorithm > 코딩테스트_합격자되기_인프런 _스터디' 카테고리의 다른 글
| [Step 8] 정렬 (2) | 2024.09.03 |
|---|---|
| [Step 7] 백트래킹 (0) | 2024.08.26 |
| [Step 5] 집합 (0) | 2024.08.11 |
| [Step 4] 트리 (0) | 2024.08.03 |
| [Step 3] 해시 (0) | 2024.07.27 |
