코테에서 정렬은 언제 필요한가?


대표적인 정렬 알고리즘
삽입 정렬
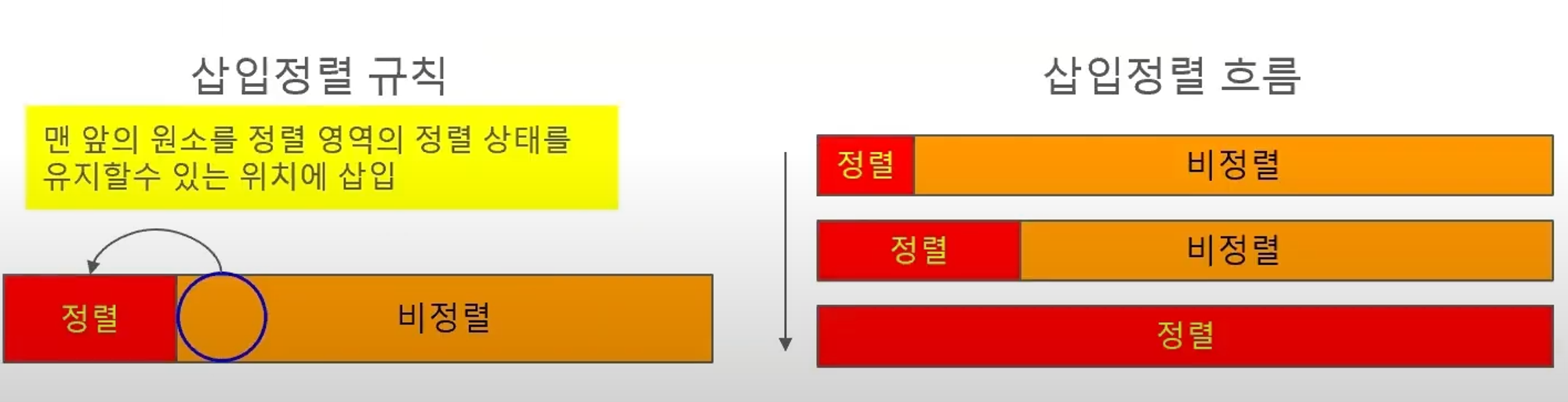
- 왼쪽 : 정렬된 영역 / 오른쪽 : 비 정렬된 영역
- 정렬된 영역이 점점 확장되어 비 정렬된 영역이 사라짐
- 비 정렬된 영역의 맨 앞의 원소를 정렬된 영역의 적절한 곳에 추가
- 용도: 작은 데이터 셋에서 효율적이며, 이미 부분적으로 정렬된 배열에서 높은 성능을 보입니다.
삽입정렬 과정
1. 첫 번째 원소를 정렬된 부분으로 간주합니다.
2. 다음 원소를 정렬된 부분과 비교하여, 올바른 위치에 삽입합니다.
3. 모든 원소가 정렬된 부분에 삽입될 때까지 2의 과정을 반복합니다.

삽입 정렬의 최고 / 최악 케이스

최선의 경우: O(n) - 이미 정렬된 배열의 경우
- 평균의 경우: O(n^2) - 일반적인 경우
- 최악의 경우: O(n^2) - 역순으로 정렬된 배열의 경우
/*
도식화 예:(아래 코드 기준)
입력 배열: [5, 2, 9, 1, 5, 6]
첫 번째 패스: [5| 2, 9, 1, 5, 6] => |의 왼쪽은 정렬된 부분
두 번째 패스: [2, 5| 9, 1, 5, 6] => 2를 정렬된 부분의 올바른 위치에 삽입
세 번째 패스: [2, 5, 9| 1, 5, 6] => 9는 이미 올바른 위치에 있음
네 번째 패스: [2, 5, 9| 1, 5, 6] => 1을 정렬된 부분의 올바른 위치, 즉 배열의 맨 앞에 삽입
다섯 번째 패스: [1, 2, 5, 9| 5, 6] => 5를 정렬된 부분의 올바른 위치, 즉 5 바로 앞에 삽입
여섯 번째 패스: [1, 2, 5, 5, 9| 6] => 6을 정렬된 부분의 올바른 위치, 즉 9 바로 앞에 삽입
완료된 정렬: [1, 2, 5, 5, 6, 9]
*/
// 삽입정렬의 슈도코드:
// for i = 1 to length(A) - 1
// key = A[i]
// j = i - 1
// while j >= 0 and A[j] > key
// A[j + 1] = A[j]
// j = j - 1
// A[j + 1] = key
#include <iostream>
#include <vector>
using namespace std;
void insertionSort(vector<int>& arr) {
int n = arr.size();
for(int i=1; i<n; i++) {
int key = arr[i];
int j = i-1;
// 정렬된 부분에서 key를 삽입할 위치를 찾는다.
while(j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
int main() {
vector<int> arr = {5, 2, 9, 1, 5, 6};
insertionSort(arr);
cout << "Sorted array: ";
for(int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
병합 정렬
- 리스트를 반으로 나눠 각각 정렬한 뒤, 합치는 방식
- 각 부분 리스트를 재귀적으로 정렬
- 최종적으로 정렬된 두 리스트를 합쳐서 전체 리스트 정렬
- 용도: 대규모 데이터 정렬에 유용 (안정 정렬)
병합정렬 과정

Conquer(병합) 과정
1. 리스트를 두 부분으로 나눕니다.
2. 각 부분을 재귀적으로 정렬합니다.
3. 두 부분을 병합하여 결과를 얻습니다.


/*
머지 정렬(Merge Sort)은 분할 정복 알고리즘의 한 예입니다.
- 시간 복잡도: O(n log n)
- 용도: 대규모 데이터 정렬에 유용 (안정 정렬)
도식화 예:
Original: [38, 27, 43, 3, 9, 82, 10]
1. Divide: [38, 27, 43, 3], [9, 82, 10]
2. Divide: [38, 27], [43, 3], [9, 82], [10]
3. Merge: [27, 38], [3, 43], [9, 82], [10]
4. Merge: [3, 27, 38, 43], [9, 10, 82]
5. Merge: [3, 9, 10, 27, 38, 43, 82]
*/
#include <vector>
#include <iostream>
using namespace std;
void merge(vector<int>& arr, int l, int m, int r) {
// Step 1: Divide the array into two halves
int n1 = m - l + 1;
int n2 = r - m;
vector<int> L(n1), R(n2);
// Step 2: Copy data to temp arrays L[] and R[]
for (int i = 0; i < n1; i++)
L[i] = arr[l + i];
for (int j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
// Step 3: Merge the temp arrays back into arr[l..r]
int i = 0, j = 0, k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// Step 4: Copy the remaining elements of L[], if there are any
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// Step 5: Copy the remaining elements of R[], if there are any
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(vector<int>& arr, int l, int r) {
if (l >= r)
return; // returns recursively
int m = l + (r - l) / 2;
mergeSort(arr, l, m); // Sort first half
mergeSort(arr, m + 1, r); // Sort second half
merge(arr, l, m, r); // Merge the sorted halves
}
int main() {
vector<int> arr = {38, 27, 43, 3, 9, 82, 10};
int arr_size = arr.size();
cout << "Given array is \n";
for(auto& num : arr) {
cout << num << " ";
}
cout << endl;
mergeSort(arr, 0, arr_size - 1);
cout << "Sorted array is \n";
for(auto& num : arr) {
cout << num << " ";
}
cout << endl;
return 0;
}
힙 정렬
- 용도: 데이터를 오름차순 또는 내림차순으로 정렬할 때 사용

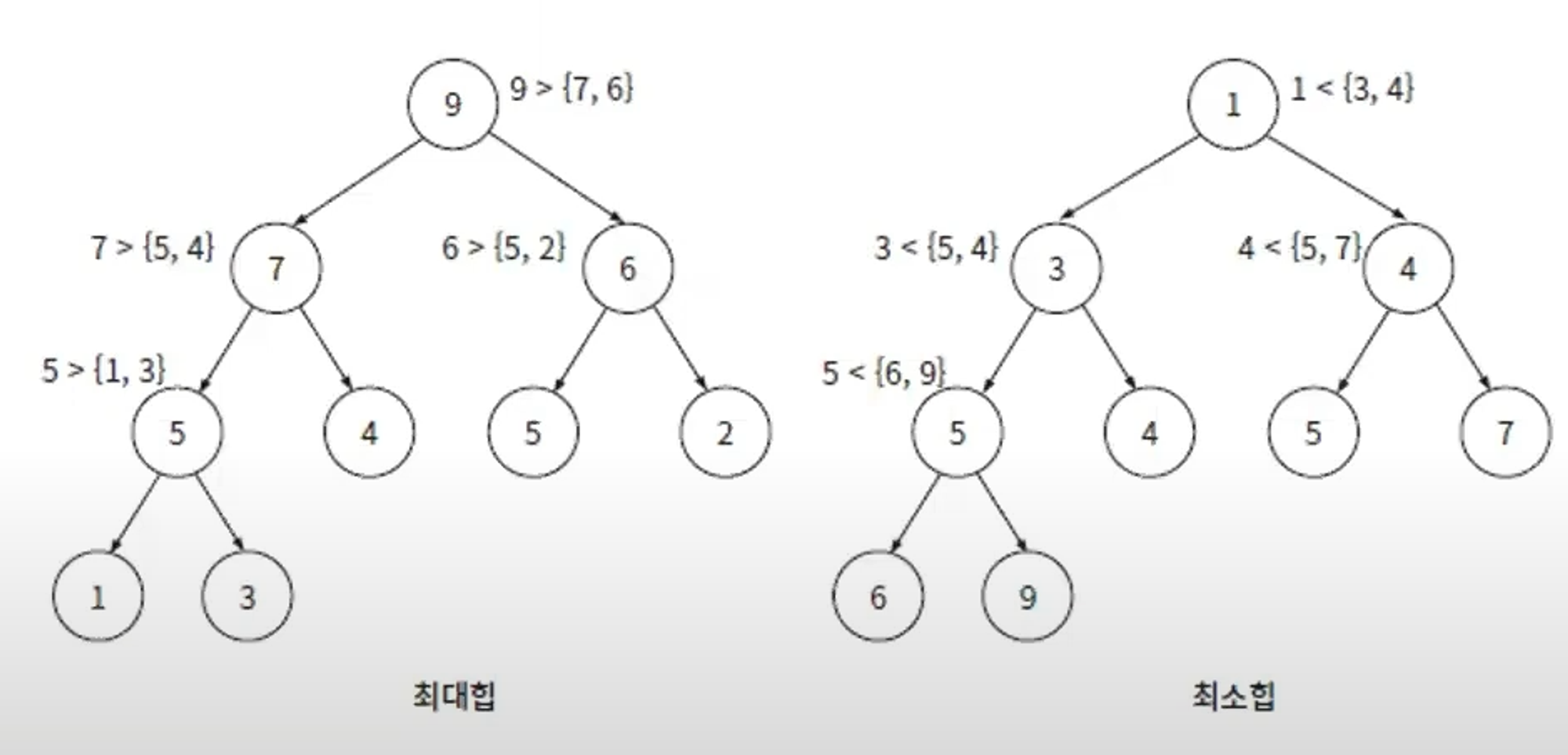
최대힙 : 부모가 항상 자식보다 큼
최소힙 : 부모가 항상 자식보다 작음
힙 구축(heapify연산)
⇒ max_heapify() 연산을 노드번호 N/2 부터 1까지 차례대로 시행
- max_heapify()연산
- 현재 노드와 자식 노드 비교(자식 노드 없으면 연산 종료)
- 현재 노드가 가장 크지(작지) 않다면 가장 큰(작은) 자식 노드의 값과 swap
- 맞바꾼 자식 노드 위치를 현재 노드로 해서 1. 부터 반복




힙 정렬
⇒ 우선순위 큐에서도 사용이 됨
- 정렬되지 않은 데이터로 최대(소) 힙 구축
- 현재 최대(소)힙의 루트노드와 마지막 노드를 맞바꿈
- 최대(소)힙 사이즈가 1이면 종료, 최대(소)힙 사이즈를 1 줄임, max_heapify(1) 수행 다시 2. 로감

/*
도식화 예:
입력 배열: [3, 1, 4, 1, 5, 9, 2, 6]
1단계: 힙 만들기
[9, 5, 4, 1, 3, 1, 2, 6]
가상의 트리 구조로 나타낼 때:
9
/ \
5 4
/| |\
1 3 1 2
/ \
6 [empty]
2단계: 정렬 과정 시작 - 루트(현재 최대값)와 마지막 노드 교환
[6, 5, 4, 1, 3, 1, 2, 9]
6
/ \
5 4
/| |\
1 3 1 2
/ \
9 [empty]
3단계: 힙 복원
[6, 5, 4, 1, 3, 1, 2, 9]
6
/ \
5 4
/| |\
1 3 1 2
/ \
9 [empty]
(동일한 힙 구조이므로 그림은 생략)
4단계: 다시 루트와 마지막 노드(현재 힙의 마지막) 교환
[2, 5, 4, 1, 3, 1, 6, 9]
2
/ \
5 4
/| |\
1 3 1 6
/ \
9 [empty]
5단계: 힙 복원
[5, 3, 4, 1, 2, 1, 6, 9]
5
/ \
3 4
/| |\
1 2 1 6
/ \
9 [empty]
... 이런 식으로 계속 과정이 진행됩니다.
완료된 정렬:
[1, 1, 2, 3, 4, 5, 6, 9]
*/
#include <iostream>
#include <vector>
using namespace std;
void heapify(vector<int>& arr, int n, int i) {
int largest = i;
int left = 2*i + 1;
int right = 2*i + 2;
if(left < n && arr[left] > arr[largest])
largest = left;
if(right < n && arr[right] > arr[largest])
largest = right;
if(largest != i) {
swap(arr[i], arr[largest]);
heapify(arr, n, largest);
}
}
void heapSort(vector<int>& arr) {
int n = arr.size();
// Build heap
for(int i = n/2 - 1; i >= 0; i--)
heapify(arr, n, i);
// Extract elements from heap
for(int i = n-1; i > 0; i--) {
swap(arr[0], arr[i]);
heapify(arr, i, 0);
}
}
int main() {
vector<int> arr = {3, 1, 4, 1, 5, 9, 2, 6};
heapSort(arr);
cout << "Sorted array: ";
for(int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
우선순위 큐
⇒ 기존 큐와는 다르게 들어온 순서와 상관 없이 우선순위가 높은 원소가 먼저 Out 됨
우선순위 큐의 구현 시 고려할 점
- 원소가 계속 들어오는 상황에서 정렬 상태를 유지 =⇒ 힙 구조 사용(기존의 정렬 상태를 유지하면서 원소삽입, 삭제 연산을 할 때 가장 빠른 연산이기 때문)
- 기존 대부분 정렬 방법은 O(NlogN)
- 힙정렬을 사용할 경우 삽입/삭제시 O(logN) 보장. ⇒ 우선순위큐는 힙을 사용
** 코테에서 우선순위 큐는 최단경로 알고리즘 (다익스트라, 밸만포드) 구현시 많이 사용 **
STL에서 제공하는 우선순위 큐
⇒ STL에서 우선순위 큐를 제공
⇒ 기본적으로 최대힙으로 동작
#include <iostream>
#include <queue>
using namespace std;
// priority_queue는 힙(기본적으로는 최대 힙)을 기반으로 한 STL 컨테이너입니다.
// - 가장 높은 우선순위를 가진 요소에 빠르게 접근할 수 있습니다.
// 좋은 사용 시기:
// - 데이터 중에서 가장 높은 (또는 낮은) 우선순위를 가진 요소에 빠르게 접근하고자 할 때.
// 성능 이슈:
// - 모든 요소를 정렬된 상태로 유지하는 것보다 우선순위 큐의 힙 구조가 더 효율적입니다.
int main() {
// priority_queue 선언 (기본적으로 최대 힙)
priority_queue<int> pq;
// push: O(log n)
pq.push(3);
pq.push(1);
pq.push(4);
// top: O(1)
cout << pq.top() << endl; // 출력: 4 (가장 높은 우선순위)
// pop: O(log n)
pq.pop();
// size: O(1)
cout << pq.size() << endl; // 출력: 2
// 순회 (힙의 순서대로, 정렬된 순서가 아님): O(n)
while(!pq.empty()) {
cout << pq.top() << " "; // 출력: 3 1
pq.pop();
}
cout << endl;
// clear: priority_queue에는 clear 메서드가 없습니다.
// 대신, 새로운 빈 큐로 교체하는 방식을 사용할 수 있습니다.
priority_queue<int> empty;
swap(pq, empty);
return 0;
}
*****************************사용자 정의 우선순위 큐 코드 예시****************************
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// 좌표를 나타내는 구조체 정의
struct Point {
int x, y;
// 비교 연산자 정의 (내림차순)
// 우선순위 큐에서 가장 큰 값을 우선 처리하기 위해 사용
bool operator<(const Point& other) const {
// 내림차순 정렬을 위해 x 좌표가 큰 순서대로,
// x 좌표가 같다면 y 좌표가 큰 순서대로 정렬
if (x == other.x) {
return y < other.y;
}
return x < other.x;
}
};
int main() {
priority_queue<Point> pq;
// 좌표 삽입
// push() 함수는 우선순위 큐에 요소를 삽입합니다.
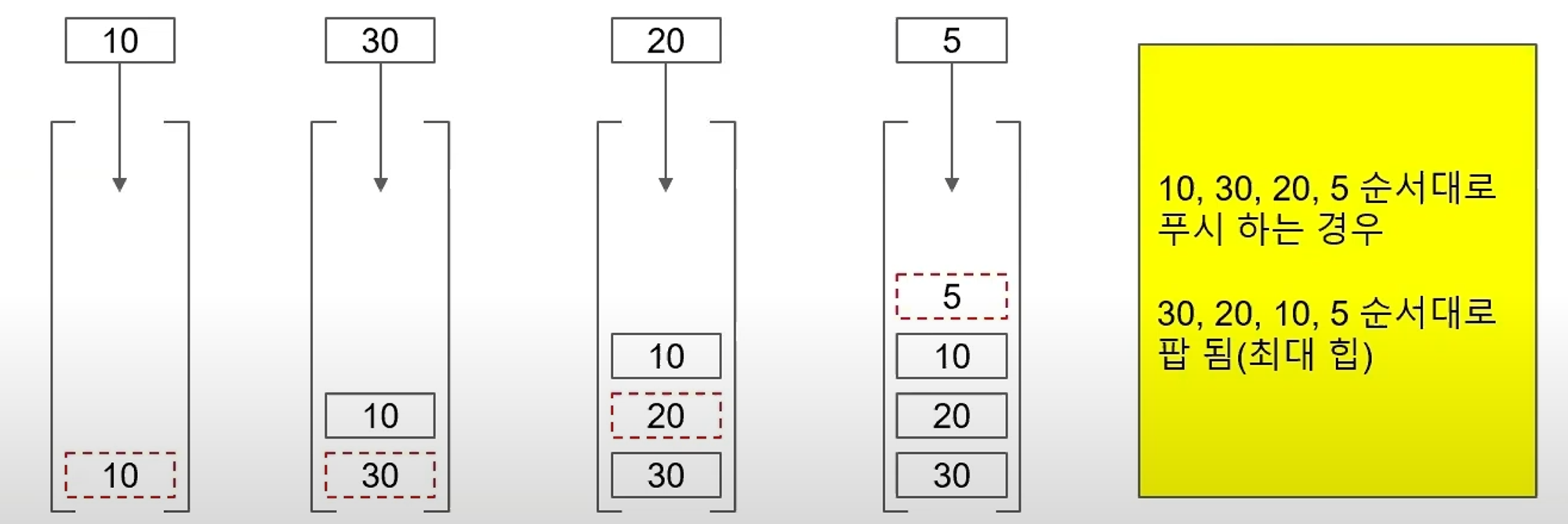
pq.push({10, 20}); // (10, 20) 삽입
pq.push({30, 40}); // (30, 40) 삽입
pq.push({20, 30}); // (20, 30) 삽입
pq.push({5, 10}); // (5, 10) 삽입
while (!pq.empty()) {
Point p = pq.top(); // 우선순위가 가장 높은 좌표를 반환
cout << "(" << p.x << ", " << p.y << ") "; // 좌표를 출력
pq.pop(); // 우선순위가 가장 높은 좌표를 큐에서 제거
}
return 0;
}
// 출력 설명:
// priority_queue는 기본적으로 최대 힙(Max-Heap) 구조로 동작하여 가장 큰 요소가
// 가장 높은 우선순위를 가집니다.
// 좌표 구조체(Point)의 비교 연산자(operator<)를 사용하여 x 좌표가 큰 순서대로,
// x 좌표가 같다면 y 좌표가 큰 순서대로 정렬됩니다.
// 따라서, 위의 코드는 (30, 40), (20, 30), (10, 20), (5, 10) 순으로 좌표를 출력합니다.
// 결과적으로, 우선순위 큐에 삽입된 좌표들은 내림차순으로 정렬되어 출력됩니다.
각 정렬 알고리즘 비교

출처
[지금 무료] 코딩 테스트 합격자 되기 - C++ 강의 | dremdeveloper - 인프런
dremdeveloper | 코딩 테스트 합격을 위한 C++ 강의, 책 없이도 가능! 저자와 직접 소통 가능한 커뮤니티 제공!, [사진]여기에 문의 하세요https://open.kakao.com/o/gX0WnTCf📘 코딩 테스트 합격자 되기 - C++편
www.inflearn.com
'Algorithm > 코딩테스트_합격자되기_인프런 _스터디' 카테고리의 다른 글
| [Step 9] 동적 계획법 (0) | 2024.09.08 |
|---|---|
| [Step 7] 백트래킹 (0) | 2024.08.26 |
| [Step 6] 그래프 (0) | 2024.08.25 |
| [Step 5] 집합 (0) | 2024.08.11 |
| [Step 4] 트리 (0) | 2024.08.03 |
