백트래킹 개념
⇒ 가장 최근에 방문했던 노드로 다시 돌아감 (DFS에서 사용한 것 처럼)
⇒ 완전 탐색하지 말고, 내가 찾는 답일 가능성이 있는 경우에만 탐색
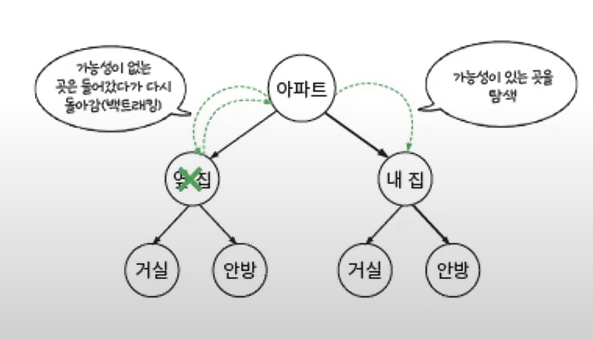
백트래킹을 푸는 과정
상태 정의 : 문제의 각 단계에서 가능한 상태를 정의.
유망함수 : 현재 상태가 유망한지 판단. 유망하지 않으면 더이상 탐색 하지 않음.
해결책 확인 : 현재 상태가 문제의 해결책인지?
재귀 호출 : 유망한 상태로 이동하면서 문제 해결 (유망할 때 DFS 진행)
/*
상태 정의 : 문제의 각 단계에서 가능한 상태를 정의
유망 함수(isPromising) : 현재 상태가 유망한지 판단, 유망하지 않으면 더 이상 탐색 x
해결책 확인(isSolution) : 현재 상태가 문제의 해결책인지 판단
재귀 호출 : 유망한 상태로 이동하면서 문제 해결
*/
// 유망성 판단 함수
bool isPromising(int level, State state) {
// 현재 상태가 유망한지 판단하는 로직을 구현합니다.
}
// 해결책 확인 함수
bool isSolution(State state) {
// 현재 상태가 문제의 해결책인지 판단하는 로직을 구현합니다.
}
// 백트래킹 함수
void backtrack(int level, State state) {
// 현재 상태가 해결책이면 처리
if (isSolution(state)) {
processSolution(state);
return;
}
// 다음 가능한 상태를 탐색
for (State nextState : possibleStates(state)) {
if (isPromising(level, nextState)) {
backtrack(level + 1, nextState);
}
}
}
백트래킹 예시
부분 합
ex) 1,2,3,4 로 이루어진 집합에서 숫자를 뽑아서 합이 5인 조합 구하기

완전 탐색으로 풀기.
⇒각 숫자를 뽑았을 경우 or 안 뽑았을 경우로 나눔
부분합을 백트래킹으로 접근하기
- 상태정의 : 현재까지 선택한 숫자들의 합
- 유망 함수 : 현재 부분 합이 목표 값을 초과하면 유망하지 않다고 판단
==> 이 문제가 유망한 경우, 유망하지 않은 경우를 나눌 수 있는 문제인가??
3. 해결책 확인 : 현재 부분 합이 목표값과 일치하는지 확인
4. 재귀 호출 : 다음 숫자를 선택하여 부분합 갱신

2=⇒ 현재 조합으로 합이 5 이상이므로 조건에 맞지 않으므로 백트래킹
1=⇒ 현재 조합으로 합이 5가 되면 더이상 탐색할 필요가 없음 백트래킹
#include <iostream>
#include <vector>
using namespace std;
// 사용할 숫자들
vector<int> nums = {1, 2, 3, 4};
// 목표 합
int target = 5;
// 현재 조합
vector<int> current; //탐색할때 현재까지의 조합
void findCombinations(int index) {// 조합수에 사용할 수를 저장
int sum = 0;
for (int num : current) {
sum += num;
}
// 조건 1: 현재 조합으로 합이 target이 되면 결과를 출력하고 더 탐색하지 않음
if (sum == target) {
for (int num : current) {
cout << num << " ";
}
cout << endl;
return;
}
// 조건 2: 합이 target을 초과하면 더 탐색하지 않음
if (sum > target) {
return;
}
// 유망한 경우에만 다음 숫자를 추가하여 탐색을 계속함
for (int i = index; i < nums.size(); ++i) {
current.push_back(nums[i]);
findCombinations(i + 1);
current.pop_back();
// 현재 숫자를 조합에서 제외하여 다음 경우를 탐색
//ex) 1 -> 2 3 4 // 2 -> 3 4 // 3 -> 4 1일때 2 3 4 조합 가능 ....
}
}
int main() {
findCombinations(0);
return 0;
}
/*
Call trace: findCombinations({ 1 }, 1, 1)
Call trace: findCombinations({ 1 2 }, 2, 2)
Call trace: findCombinations({ 1 2 3 }, 3, 3)
Pruned branch: sum(6) > target(5)
// Pruned branch: 현재 합이 목표 값보다 크므로 더 이상 탐색 하지 않음.
Call trace: findCombinations({ 1 2 4 }, 4, 3)
Pruned branch: sum(7) > target(5)
// Pruned branch: 현재 합이 목표 값보다 크므로 더 이상 탐색하지 않음.
Call trace: findCombinations({ 1 3 }, 3, 2)
Call trace: findCombinations({ 1 3 4 }, 4, 3)
Pruned branch: sum(8) > target(5)
// Pruned branch: 현재 합이 목표 값보다 크므로 더 이상 탐색하지 않음.
Call trace: findCombinations({ 1 4 }, 4, 2)
Found combination: { 1 4 }
/** Found combination: 현재 합이 목표 값과 일치하므로 조합을 출력하고 백트래킹함.**/
Call trace: findCombinations({ 2 }, 2, 1)
Call trace: findCombinations({ 2 3 }, 3, 2)
Found combination: { 2 3 }
/** Found combination: 현재 합이 목표 값과 일치하므로 이 조합을 출력하고 백트래킹함.**/
Call trace: findCombinations({ 2 4 }, 4, 2)
Pruned branch: sum(6) > target(5)
// Pruned branch: 현재 합이 목표 값보다 크므로 더 이상 탐색하지 않음.
Call trace: findCombinations({ 3 }, 3, 1)
Call trace: findCombinations({ 3 4 }, 4, 2)
Pruned branch: sum(7) > target(5)
// Pruned branch: 현재 합이 목표 값보다 크므로 더 이상 탐색하지 않음.
Call trace: findCombinations({ 4 }, 4, 1)
*/
N 퀸
⇒ 체스의 퀸을 N * N 체스판에 N개 배치했을 때 서로 공격할 수 없는 위치에 놓을 수 있는 방법의 수 확인

N 퀸을 백트래킹으로 접근하기
- 상태 정의 : 각 행에 하나의 퀸이 위치하도록 함
- 유망 함수 : 현재 행에 퀸을 놓았을 때, 다른 퀸과 충돌하는지 확인
- 해결책 확인 : 모든 퀸이 배치되었는지 확인
- 재귀 호출 : 다음행에 퀸을 배치
N퀸을 완전탐색으로 푸는 경우

N * N 의 크기 체스판에 N개의 퀸을 놓는 경우의 수는 O(N^N) 모든 경우의 수를 따져봐야 한다.
⇒ 효율 최악!
N퀸 , 개선 아이디어
일단 각 행에 퀸 하나씩 배치한다.
1. 각 행의 동일한 열에 퀸이 배치되지 않도록 함

⇒ 각 행의 열위치를 1차원 배열에 저장함
만일 동일한 값이 있으면 특정 열 위치에 중복되는 퀸이 있다는 것이므로 백트래킹
2. 각 행의 퀸들이 대각선 방향에 겹치지 않도록 함
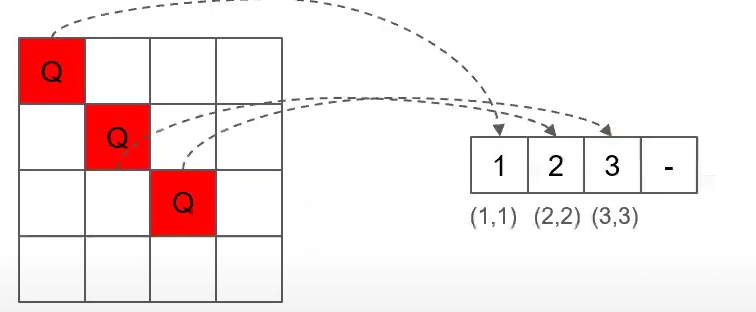



- 결론!
1. 각행의 동일한 열에 퀸이 배치되지 않도록함
⇒ 각 열의 값이 같은지 확인
2. 각행의 대각선 위치에 퀸이 배치되지 않도록함
⇒ 행과 열의 절대값 차가 같은지 확인하자! (왼쪽, 오른쪽 대각선 동일)
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
// N Queen 문제: n x n 체스판에 n개의 퀸을 서로 공격하지 못하게 배치하는 문제
const int N = 4; // 퀸의 개수
vector<int> board(N, -1); // 보드 배열, 인덱스는 행을, 값은 열을 나타냄
// 보드의 현재 상태를 출력하는 함수
void printBoard() {
// 각 행을 반복
for (int i = 0; i < N; ++i) {
// 각 열을 반복
for (int j = 0; j < N; ++j) {
// 현재 위치에 퀸이 있는지 확인
if (board[i] == j) {
cout << "Q "; // 퀸이 있으면 "Q" 출력
} else {
cout << ". "; // 퀸이 없으면 "." 출력
}
}
cout << endl; // 한 행이 끝나면 줄바꿈
}
cout << endl; // 보드 전체 출력 후 줄바꿈
}
// 현재 위치에 퀸을 놓아도 되는지 확인하는 유망함수
bool isSafe(int row, int col) {
// 현재 행 이전의 모든 행을 검사
for (int i = 0; i < row; ++i) {
// 1. 같은 열에 퀸이 있는지 확인
if (board[i] == col) {
return false; // 같은 열에 퀸이 있으면 false 반환
}
// 2. 같은 대각선에 퀸이 있는지 확인
if (abs(board[i] - col) == abs(i - row)) {
return false; // 같은 대각선에 퀸이 있으면 false 반환
}
}
return true; // 어떤 충돌도 없으면 true 반환
}
// N Queen 문제를 해결하기 위한 재귀 함수
void solveNQueens(int row, int &solutions) {
// 모든 행에 퀸을 배치한 경우 (기저 조건)
if (row == N) {
// 해결책을 찾았으므로 해결책 수 증가
solutions++;
// 현재 보드 상태를 출력
printBoard();
return; // 함수 종료
}
// 현재 행의 모든 열에 대해 반복
for (int col = 0; col < N; ++col) {
// 현재 위치에 퀸을 놓을 수 있는지 확인
if (isSafe(row, col)) {
board[row] = col; // 현재 행의 열에 퀸을 놓음
solveNQueens(row + 1, solutions); // 다음 행에 대해 재귀 호출
// 퀸을 제거할 필요 없음, 다음 반복에서 덮어쓰기 때문에
}
}
}
int main() {
int solutions = 0; // 해결책 수를 저장할 변수
solveNQueens(0, solutions); // 첫 번째 행부터 시작
cout << "총 해결책 수: " << solutions << endl; // 총 해결책 수 출력
return 0;
}
/*
. Q . .
. . . Q
Q . . .
. . Q .
. . Q .
Q . . .
. . . Q
. Q . .
총 해결책 수: 2
*/
출처
[지금 무료] 코딩 테스트 합격자 되기 - C++ 강의 | dremdeveloper - 인프런
dremdeveloper | 코딩 테스트 합격을 위한 C++ 강의, 책 없이도 가능! 저자와 직접 소통 가능한 커뮤니티 제공!, [사진]여기에 문의 하세요https://open.kakao.com/o/gX0WnTCf📘 코딩 테스트 합격자 되기 - C++편
www.inflearn.com
'Algorithm > 코딩테스트_합격자되기_인프런 _스터디' 카테고리의 다른 글
| [Step 9] 동적 계획법 (0) | 2024.09.08 |
|---|---|
| [Step 8] 정렬 (2) | 2024.09.03 |
| [Step 6] 그래프 (0) | 2024.08.25 |
| [Step 5] 집합 (0) | 2024.08.11 |
| [Step 4] 트리 (0) | 2024.08.03 |
