트리 개념

⇒ 노드와 간선으로 이루어진 계층적 자료구조. (부모- 자식 관계)
⇒ 순환을 허용하지 않음.
⇒ 코테에서는 이진트리(자식 노드가 최대 2개인 트리)만 알면 됨.
이진 트리 표현하기
1. 배열

루트 노트 인덱스 = 1
왼쪽 자식 노드는 부모노드 인덱스 *2
오른쪽 자식 노드는 부모노드 인덱스 * 2 +1
2. 인접 리스트

⇒각 리스트의 인덱스는 부모 노드
⇒자식 노드는 부모 노드에 해당되는 인덱스에 추가
이진 트리 순회
1. 전위순회 (부모 → 왼쪽 자식 → 오른쪽 자식)

#include <iostream>
using namespace std;
// 트리를 배열로 나타내기 위해서, 배열의 인덱스를 사용하는 후위 순회 함수 정의
void postorderTraversal(int tree[], int index, int size) {
if (index >= size || tree[index] == -1) return;
// 유효하지 않은 인덱스나 값이 -1이면 종료
//끝까지 트리를 순회하면 끝.
// Step 1: 현재 노드 값 출력
cout << tree[index] << " ";
// Step 2: 왼쪽 자식 노드로 이동 (2*index)
postorderTraversal(tree, 2 * index/*왼쪽자식노드*/, size);
// Step 3: 오른쪽 자식 노드로 이동 (2*index + 1)
postorderTraversal(tree, 2 * index + 1/*오른쪽 자식 노드*/, size);
}
int main() {
// 트리를 배열로 나타내기
// -1은 해당 위치에 노드가 없음을 나타냅니다.
int tree[] = {-1, 1, 4, 8, 3, 5, -1, 7, 2, -1, -1, -1, -1, -1, 6};
int size = sizeof(tree) / sizeof(tree[0]);
// 후위 순회 함수 호출
postorderTraversal(tree, 1, size);
return 0;
}
//괄호안은 인덱스
1 (1)
/ \
4 (2) 8 (3)
/ \ \
3 (4) 5 (5) 7 (7)
/ /
2 (8) 6 (14)
1->4->3->2->5->8->7->6
1.1 전위 순회 예시

- 트리 복사
⇒ 전위 순회를 사용하여 트리 복사
⇒ 루트노드부터 트리 노드를 순차적으로 복사 가능
⇒ 1 4 3 2 5 8 7 6 순서대로 복사. (부모부터 차례대로 복사됨)
2. 중위순회 (왼쪽 자식 → 부모 → 오른쪽 자식)

1 ⇒ “1" 에서부터 계속 체크하면서 내려와 “2” 로 오면 왼쪽 자식이 없고 그 다음이 부모 노드 확인했을 때 “2” 이므로 “2”를 방문
4 ⇒ “4”에 도달했을 때 “3”은 이미 방문. 따라서 오른쪽 자식인 “5”를 방문
7 ⇒ “8”은 왼쪽 자식이 없으므로 “7”건너뛰고 “6”이 “7”의 왼쪽 자식이므로 “6”방문. 후에 마지막으로 “7” 방문
void inorderTraversal(int tree[], int index, int size) {
if (index >= size || tree[index] == -1) return; // 유효하지 않은 인덱스나 값이 -1이면 종료
// Step 1: 왼쪽 자식 노드로 이동 (2*index)
inorderTraversal(tree, 2 * index, size);
// Step 2: 현재 노드 값 출력
cout << tree[index] << " ";
//중위순회는 출력하는 순서만 다름 전위 순회랑 코드 이부분
//만 빼고 동일
// Step 3: 오른쪽 자식 노드로 이동 (2*index + 1)
inorderTraversal(tree, 2 * index + 1, size);
}
2.1 중위순회 예시
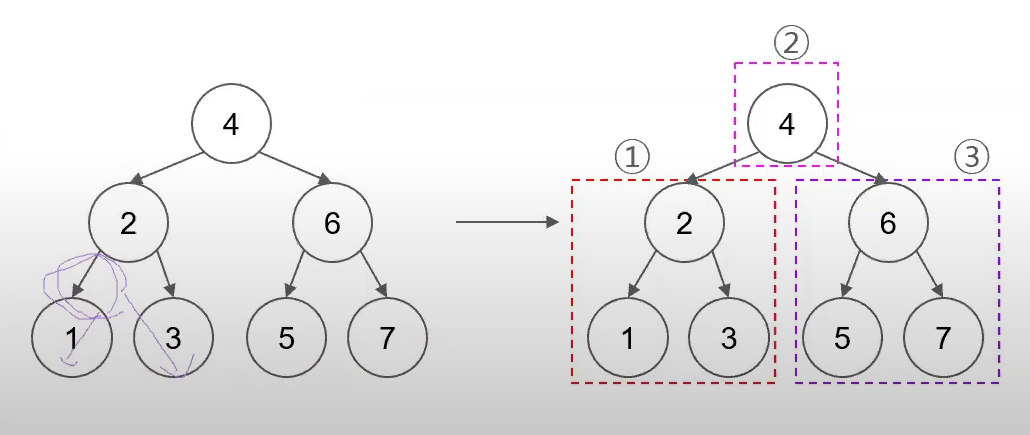
⇒이진 탐색트리의 원소를 정렬된 상태로 순회. (왼쪽 자식 <부모 , 오른쪽 자식 > 부모)
1→2→3→4→5→6→7
3. 후위순회 (왼쪽 자식 → 오른쪽 자식 → 부모)

// 트리를 배열로 나타내기 위해서, 배열의 인덱스를 사용하는 후위 순회 함수 정의
void postorderTraversal(int tree[], int index, int size) {
if (index >= size || tree[index] == -1) return; // 유효하지 않은 인덱스나 값이 -1이면 종료
// Step 1: 왼쪽 자식 노드로 이동 (2*index)
postorderTraversal(tree, 2 * index, size);
// Step 2: 오른쪽 자식 노드로 이동 (2*index + 1)
postorderTraversal(tree, 2 * index + 1, size);
// Step 3: 현재 노드 값 출력
cout << tree[index] << " ";
}
2.1 후위순회 예시
폴더 삭제하기, 트리 삭제

⇒ 제일 깊숙이 들어가 있는 폴더부터 삭제
⇒ 트리를 삭제할 때 사용.
이진 탐색 트리
⇒탐색을 효율적으로 하기 위해 만든 이진 트리
⇒왼쪽 자식 < 부모노드 // 오른쪽 자식 > 부모노드
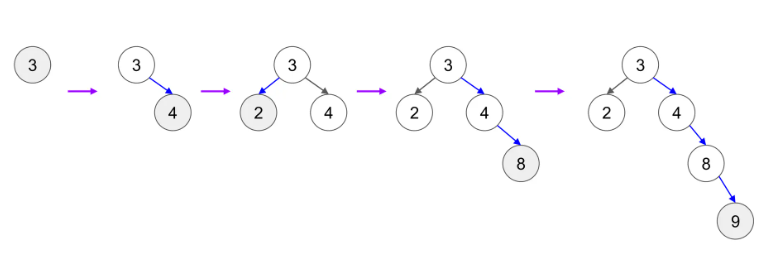
⇒ 데이터가 크기 순으로 왼쪽 오른쪽으로 들어감.
이진탐색 트리를 활용한 탐색의 효율

최대 탐색 횟수 : 트리 높이와 같음 ( 최악의 경우 O(N) → 오른쪽, 균형 유지시 O(NlogN)→ 왼쪽)
삽입과 동시에 정렬.
map, set의 내부는 균형 이진탐색트리로 되어있음.=⇒ 키값 기준 정렬 o
unordered는 해시 =⇒ 키값 기준 정렬 x
출처
[지금 무료] 코딩 테스트 합격자 되기 - C++ 강의 | dremdeveloper - 인프런
dremdeveloper | 코딩 테스트 합격을 위한 C++ 강의, 책 없이도 가능! 저자와 직접 소통 가능한 커뮤니티 제공!, [사진]여기에 문의 하세요https://open.kakao.com/o/gX0WnTCf📘 코딩 테스트 합격자 되기 - C++편
www.inflearn.com
'Algorithm > 코딩테스트_합격자되기_인프런 _스터디' 카테고리의 다른 글
| [Step 6] 그래프 (0) | 2024.08.25 |
|---|---|
| [Step 5] 집합 (0) | 2024.08.11 |
| [Step 3] 해시 (0) | 2024.07.27 |
| [Step 2] 스택/큐 (2) | 2024.07.20 |
| [Step 1.5] 코딩 테스트에서 꼭 알아야 할 C++ 문법 (0) | 2024.07.18 |
